怎样算自己的星座,如何准确算自己星座
怎样算自己的星座目录
怎样算自己的星座
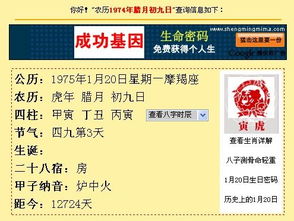
要计算自己的星座,可以按照以下步骤进行:
1. 确定阳历出生日期:首先需要知道自己的阳历(公历)出生日期,这是判断星座的基础[[4]]。
2. 对照星座日期范围:根据阳历出生日期,对照星座的日期范围来确定自己的星座。例如:
白羊座:3月21日 4月20日
金牛座:4月21日 5月20日
双子座:5月21日 6月21日
巨蟹座:6月22日 7月22日
狮子座:7月23日 8月22日
处女座:8月23日 9月22日
天秤座:9月23日 10月22日
天蝎座:10月23日 11月21日
射手座:11月22日 12月21日
摩羯座:12月22日 1月19日
水瓶座:1月20日 2月18日
双鱼座:2月19日 3月20日[][[4]][[12]]。
3. 使用万年历转换阴历生日:如果你只知道阴历(农历)生日,可以通过查询万年历将阴历生日转换为对应的阳历生日[]。
通过以上方法,你可以准确地知道自己属于哪个星座。
如何准确算自己星座

要准确计算自己的星座,可以按照以下步骤进行:1. 确定出生日期和时间:首先需要知道自己的出生年、月、日和具体时间(最好是精确到分钟)[]。这是计算星座的基础信息。2. 查找太阳星座日期:每个星座都有一个日期范围。例如,白羊座的日期范围是3月21日至4月19日,金牛座是4月20日至5月20日,双子座是5月21日至6月21日,巨蟹座是6月22日至7月22日,狮子座是7月23日至8月22日,处女座是8月23日至9月22日,天秤座是9月23日至10月22日,天蝎座是10月23日至11月21日,射手座是11月22日至12月21日,摩羯座是12月22日至1月19日,水瓶座是1月20日至2月18日,双鱼座是2月19日至3月20日[[7]][[8]]。3. 考虑太阳在黄道上的实际位置:天文学家根据太阳在黄道上的实际位置,结合古代传下来的星座界限,确定每个星座的时间范围。由于太阳在黄道上的速度并不均匀,所以各星座的日期会有所变动[[5]][[9]]。4. 使用在线工具或计算器:可以通过输入出生年月日和时间到在线星座计算器中来快速得出自己的星座[[15]]。通过以上步骤,可以较为准确地计算出自己的星座。需要注意的是,虽然有些方法如身份证号匹配可以简化计算过程,但这些方法可能不够精确,因为它们通常基于固定的日期范围[[4]]。因此,最准确的方法还是根据具体的出生日期和时间来计算。
怎样知道自己是什么星座

要知道自己是什么星座,首先需要知道自己的阳历出生日期。星座是根据太阳在黄道带上的位置来划分的,而黄道带是由地球上看太阳运行的轨道决定的[]。每个星座都有一个对应的时间范围,例如白羊座是3月21日至4月19日,金牛座是4月20日至5月20日,双子座是5月21日至6月20日等[[7]][[9]][[13]]。具体步骤如下:1. 确定自己的阳历出生日期。2. 根据阳历日期对照星座表,确定自己属于哪个星座。例如,如果你的出生日期是4月25日,那么你就是金牛座[[7]][[9]][[13]]。有些应用程序和工具也可以帮助你快速识别自己的星座,例如Star Walk等观星应用程序[][[20]]。这些工具可以通过输入你的出生日期或查看星空照片来自动识别你的星座[[17]]。了解自己的星座主要是通过查看阳历出生日期,并对照星座表来确定的[][[6]][[8]]。
怎么看自己的上升星座
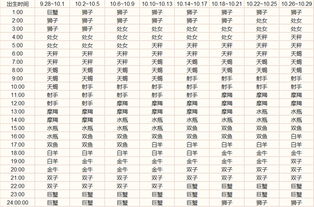
要查看自己的上升星座,首先需要了解上升星座的定义和作用。上升星座(Ascedat)是占星学中一个重要的概念,表示一个人出生时东方地平线上升时的星座位置[]。它与个人的性格、人际关系和生活经历产生重要影响[]。确定上升星座的方法如下:1. 获取出生时间和地点:你需要知道自己的出生日期、时间和地点。这些信息对于计算上升星座至关重要[[10]][[29]]。2. 使用在线计算器:有许多在线工具可以帮助你查询上升星座。只需输入你的出生日期、时间和地点,即可轻松计算出你的上升星座[[15]][[23]]。3. 咨询专业占星师:如果你希望更深入地了解自己的上升星座,可以咨询专业的占星师。他们可以根据你的出生时间提供详细的解释和分析[[15]]。4. 查阅上升星座查询表:一些网站提供了上升星座查询表,你可以通过对照出生时间来确定自己的上升星座[[27]]。了解自己的上升星座需要精确的出生时间和地点,并可以通过在线工具或专业占星师的帮助来实现。上升星座在占星学中具有重要意义,能够帮助你更好地理解自己的外在表现和行为方式[][[7]][[20]]。
