一、几何八字形的定义与特征

几何八字形，顾名思义，是一种具有八字形状的几何图形。它通常由两条相互垂直的直线相交于一点，然后分别向两侧延伸，形成类似“八”字的结构。在几何学中，八字形是一种特殊的四边形，其特点是具有两个对角线，且对角线相互垂直。

二、八字形的性质与应用

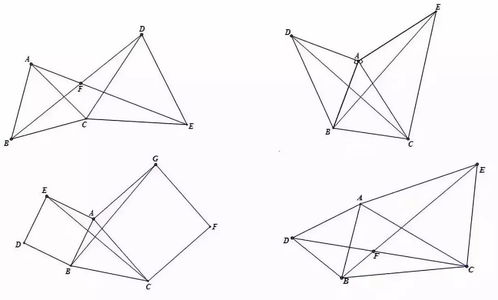
八字形的性质主要体现在以下几个方面：

对角线相互垂直：这是八字形最显著的特征，也是其名称的由来。

对角线等长：在等腰八字形中，两条对角线长度相等。

对角线平分：八字形的对角线将四边形平分为四个面积相等的三角形。

八字形在几何学中的应用十分广泛，以下列举几个例子：

在解析几何中，八字形可以用来表示直线与坐标轴的交点。

在平面几何中，八字形可以用来证明某些几何定理，如勾股定理。

在工程学中，八字形可以用来设计桥梁、水闸等结构。

三、八字形的分类与变体

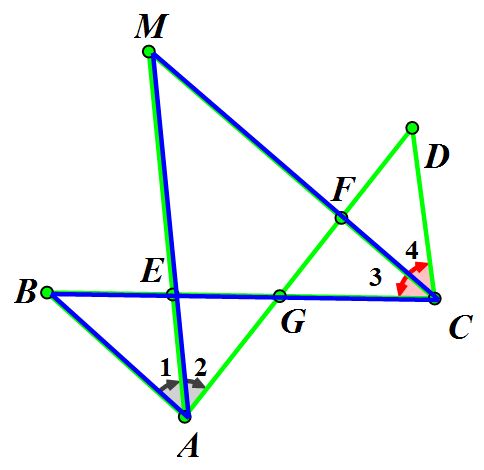
根据八字形的形状和性质，可以将其分为以下几类：

等腰八字形：两条对角线长度相等，且对角线平分。

不等腰八字形：两条对角线长度不相等，但仍然相互垂直。

斜八字形：对角线不垂直，但仍然相互交叉。

八字形还可以通过旋转、平移等变换得到各种变体，如：

旋转八字形：将八字形绕其中心旋转一定角度得到的图形。

平移八字形：将八字形沿某一方向平移一定距离得到的图形。

四、八字形的计算方法

在解决与八字形相关的问题时，以下计算方法可供参考：

面积计算：对于等腰八字形，其面积可以通过对角线长度的一半乘以对角线长度的一半再乘以根号2来计算。

周长计算：对于等腰八字形，其周长可以通过对角线长度之和乘以根号2来计算。

角度计算：对于八字形，可以通过对角线之间的夹角来计算其他角度，如内角、外角等。

五、八字形在生活中的应用

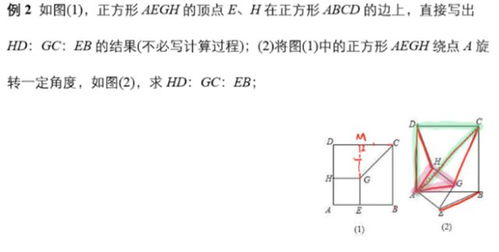
八字形不仅在数学和工程学中有着广泛的应用，在日常生活中也随处可见。以下列举几个例子：

道路设计：八字形可以用来设计道路的转弯处，提高行车安全。

建筑设计：八字形可以用来设计建筑物的入口、窗户等，使建筑更具美感。

家具设计：八字形可以用来设计家具的形状，如椅子、桌子等，使家具更具实用性。

六、总结

几何八字形是一种具有独特形状和性质的几何图形，它在数学、工程学以及日常生活中都有着广泛的应用。通过对八字形的深入研究，我们可以更好地理解和运用这一图形，为我们的生活带来便利。