深入解析数学八字图：几何模型中的独特结构

在几何学中，八字图是一种常见的几何模型，它以其独特的结构在数学教育中扮演着重要角色。本文将深入探讨八字图的概念、性质以及其在数学中的应用。

标签：八字图定义

我们来明确什么是八字图。八字图是由两条直线相交形成的图形，这两条直线在交点处形成四个角，这四个角中，相对的两个角互为对顶角，且相等。八字图因其形状类似“八”字而得名。

标签：八字图性质

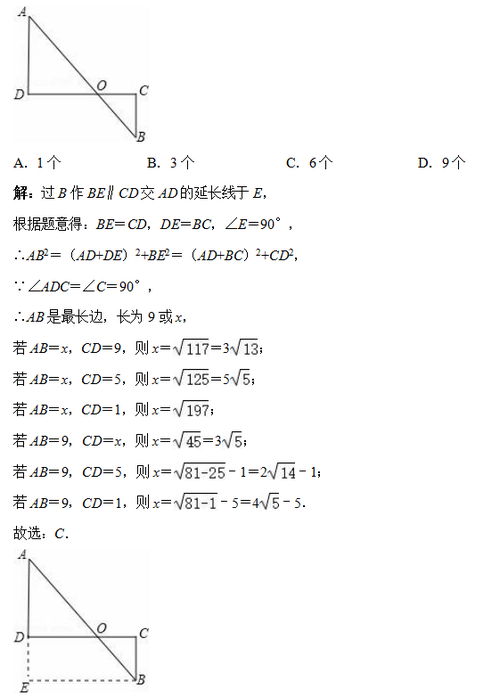
八字图具有以下性质：

对顶角相等：这是八字图最基本的一个性质，即两条相交直线形成的四个角中，相对的两个角相等。

内角和为360度：八字图的内角和等于360度，这是平面几何中所有四边形的基本性质。

外角和为360度：八字图的外角和也等于360度，这是由内角和的性质推导出来的。

标签：八字图的应用

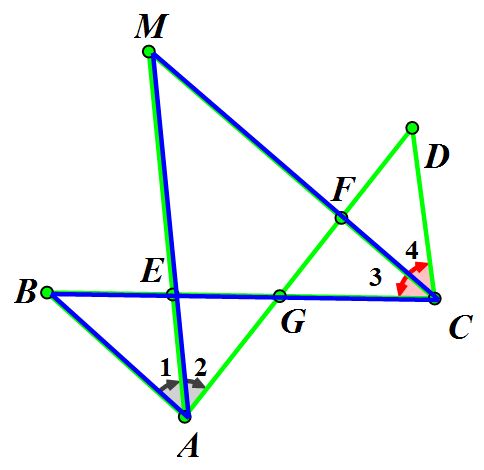
八字图在数学中的应用非常广泛，以下是一些具体的应用场景：

证明几何性质：利用八字图可以证明许多几何性质，如对顶角相等、内角和为360度等。

解决几何问题：在解决一些几何问题时，可以借助八字图来简化问题，如计算角度、求线段长度等。

辅助教学：在数学教学中，八字图可以作为辅助工具，帮助学生更好地理解几何概念和性质。

标签：八字图的构造方法

构造八字图的方法有很多，以下列举几种常见的构造方法：

使用直尺和圆规：首先画一条直线，然后以这条直线为边，画一个圆，再以圆上的任意两点为端点，画一条直线，这两条直线相交于一点，就得到了一个八字图。

利用平行线：首先画一条直线，然后在这条直线上取一点，以这个点为圆心，任意长度为半径，画一个圆，接着以这个圆上的任意两点为端点，画一条直线，这条直线与原来的直线相交，就得到了一个八字图。

利用等腰三角形：首先画一个等腰三角形，然后以底边的中点为圆心，以底边的一半为半径，画一个圆，接着以圆上的任意一点为圆心，以底边的一半为半径，画一个圆，这两个圆相交于一点，连接这个点与等腰三角形的顶点，就得到了一个八字图。

标签：八字图的实际应用

八字图在实际生活中也有许多应用，以下列举几个例子：

建筑设计：在建筑设计中，八字图可以用来计算建筑物的角度和尺寸。

城市规划：在规划城市道路时，八字图可以用来确定道路的转弯角度和半径。

机械设计：在机械设计中，八字图可以用来计算机械部件的角度和尺寸。

标签：八字图的总结

八字图是一种重要的几何模型，它在数学教育、实际应用以及生活中都发挥着重要作用。通过对八字图的学习和掌握，我们可以更好地理解几何学的概念和性质，提高我们的数学素养。